The choice of which angle to turn in producing a Koch snowflake may be determined by using a 2-adic valuation (mod 2). Other interesting curves, many with central symmetry, may be produced by using a p-adic valuation (mod 2) to determine angle choices, where p is a positive integer.

Koch curve

Created recursively: $${\sf F}\ +\!60\ \ {\sf F}\ +\!240\ \ {\sf F}\ +\!60\ \ {\sf F}$$
Created iteratively: $${\sf F}\ +\theta_1\ \ {\sf F}\ +\theta_2\ \ {\sf F}\ +\theta_3\ \ {\sf F}\ \ldots\ {\sf F}\ +\theta_k\ \ {\sf F}\ \ldots$$ $$\theta_k=\begin{cases}+60 & \text{if }\nu_2(k)\text{ is even}\\ +240 & \text{if }\nu_2(k)\text{ is odd}\end{cases}$$
$\nu_2(k)$ is the 2-adic valuation of $k$ — that is, the highest power of 2 dividing $k.$

The parity of the 2-adic valuation determines the angle; that is, the 2-adic valuation modulo 2.

Symmetric variation on the Koch curve

Created recursively: $${\sf F}\ +\!40\ \ {\sf F}\ +\!60\ \ {\sf F}\ +\!40\ \ {\sf F}$$
Angles $\alpha_0=40$ and $\alpha_1=60$ are solutions to: $$3\alpha_0+\alpha_1\equiv180\text{ mod }360$$

Using a 6-adic valuation modulo 2

6-adic valuation modulo 2: $$0\ 0\ 0\ 0\ 0\ 1\ \ 0\ 0\ 0\ 0\ 0\ 1\ \ 0\ 0\ 0\ 0\ 0\ 1$$ $$0\ 0\ 0\ 0\ 0\ 1\ \ 0\ 0\ 0\ 0\ 0\ 1\ \ 0\ 0\ 0\ 0\ 0\ 0$$
Angles: $$\alpha_0=210\ \ \text{and}\ \ \alpha_1=150$$

The same 6-adic valuation modulo 2

Angles: $$\alpha_0=210\ \ \text{and}\ \ \alpha_1=150$$
Segment lengths (cyclically): $$2.8,\ 1.03,\ 1.41,\ 1.41,\ 1.03,\ 2.8$$

4-adic valuation modulo 2

4-adic valuation modulo 2: $$0\ 0\ 0\ 1\ \ 0\ 0\ 0\ 1\ \ 0\ 0\ 0\ 1\ \ 0\ 0\ 0\ 0\ $$ $$0\ 0\ 0\ 1\ \ 0\ 0\ 0\ 1\ \ 0\ 0\ 0\ 1\ \ 0\ 0\ 0\ 0\ $$
Angles: $$\alpha_0=0\ \ \text{and}\ \ \alpha_1=120$$

2-adic $+$ 8-adic valuations modulo 2

Angles: $$\alpha_0=150\ \ \text{and}\ \ \alpha_1=210$$
Segment lengths (cyclically): $$7,\ 7,\ 4,\ -7$$

Recursive schemes with three angles

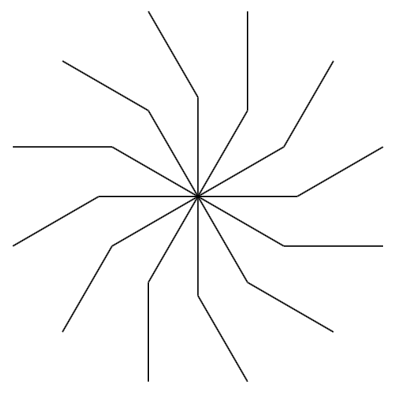
Recursive scheme: $${\sf F}\ +\!30\ \ {\sf F}\ +\!180\ \ {\sf F}\ +\!330\ \ {\sf F}$$
Number of segments needed to render a complete image: $$5,\!592,\!406$$

Additional examples: Visit www.vincematsko.com > art

Go there now!